Time after time, brilliant scientists make claims about science’s future that prove completely wrong. In a quote often misattributed to Lord Kelvin, Albert Michelson famously declared that “there is nothing new to be discovered in physics now; all that remains is more and more precise measurement.” Classical mechanics, the tradition of physics that originated with Newton, Kepler, and Galileo, is often seen as something we already understand, and something we have understood for a long time. This is simply not true. Even today, new discoveries made with classical mechanics are transforming the world of science as we know it.
In a recent breakthrough, a Yale physics lab shows new behaviors in a phenomenon that some had considered fully understood. Associate professor of physics Jack Harris and post-doctoral researcher Haitan Xu report in Nature their use of ultra-precise lasers and tiny vibrating sheets that appear to violate classical predictions. Their experiment, transferring energy by very slowly tuning the vibrations, has major implications for a decades-old theorem in mechanics: the adiabatic theorem. This newly discovered phenomenon occurs in all systems with friction, and may fundamentally shift the way physicists view systems.
A dance for the ages
Although Xu’s research focuses on how energy can be transferred between two different regions, the core of this new research deals with systems, a very general way of describing things that interact. Most things in the world are systems: the traffic through a busy city, the movement of the planets, or even a large ballroom dance.
In a ballroom dance, each person on the dance floor obeys the rules of the dance, and as they move, they interact with other people harmoniously. There might be a set number of dance moves that eventually bring them back to the starting point. Essentially, Xu’s research found that there are certain moves that when danced “clockwise,” return you to the same position, but when danced “counter-clockwise,” present you with a new partner. This non-symmetrical form has serious implications for any system, and offers a new way that scientists could control these systems.
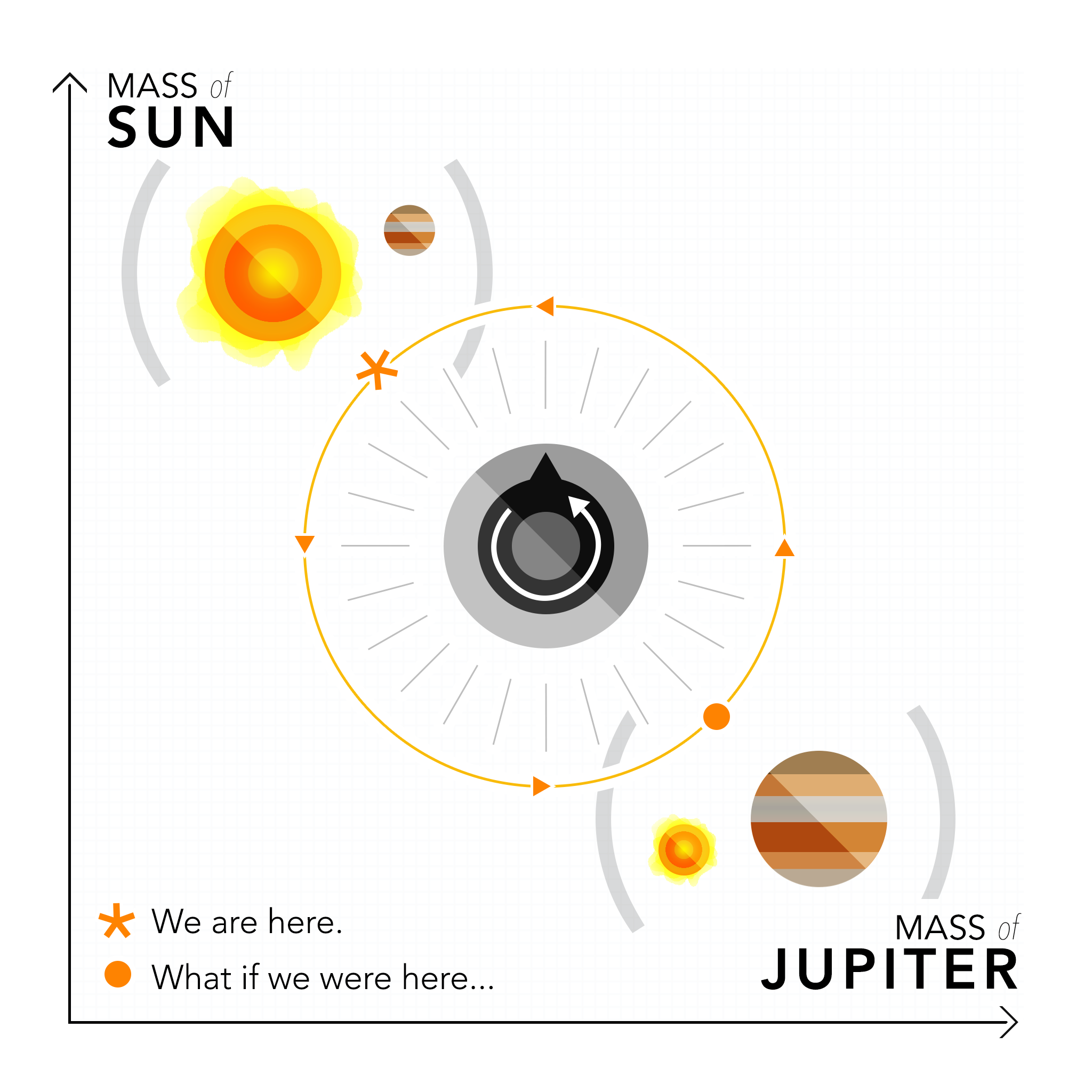
The research provides an extension of the adiabatic theorem, a theorem that governs how systems change as the parameters of the systems change. These parameters can be any controlled quality of the system — the dance moves performed, the tension in a wire, or the controls in a computer. The adiabatic theorem says that if the parameters are slowly restored to their original state, the system will appear to have not changed at all. This is very powerful in physics, because for a certain experiment on a system, scientists can restore previous states without being concerned exactly in what way the parameters changed. Yet, it is not very exciting. After all, you only end up where you begin.
Imagine for a moment that we had a small dial allowing us to change the masses of Jupiter and the Sun. Through our understanding of the laws of gravity, we could predict how the orbits of the planet change if Jupiter became more massive and if the Sun became less massive. The paths of the planets may become chaotic, but the adiabatic theorem provides a simple solution: when all of the parameters are back to where they began, the system would appear to have never changed.
However, there is one caveat to the above examples. The only way that the adiabatic theorem has been proven is through assuming systems that do not have any friction, or energy loss. Only in those cases does the adiabatic theorem work as expected. Still, physicists applied this theorem to systems with friction by assuming such systems would behave very similarly to those without friction. What physicists did not expect, however, was that the system could change completely. Although mathematicians predicted anomalies using what they called “exceptional points,” physicists were unable to see these anomalies in actual systems — until now.
Tiny vibrating membranes
While the previous systems may be simple to imagine, they would be nearly impossible to actually control and measure. In order to actually see the effects of the adiabatic theorem, Xu’s research involved vibrating a tiny membrane between two mirrors while using lasers both to control and to measure the vibrations of the membrane. The reason this is considered a system is because the membrane has two vibrational modes, or methods of vibration, and the frequency of each vibration can be controlled by the laser. Vibrational modes are like vertical waves and a horizontal waves that pass by each other, and can be thought of as two separate strings, each vibrating independently.
Vibrating strings are familiar to anyone who has played a string instrument, whether it be a guitar, a violin, or an erhu. When you pluck a single string, the other strings do not react, as each string has a different resonating frequency. However, if you tune two strings to have the same resonating frequency, the vibrating energy can transfer from one string to the other. In this experiment, the resonating frequencies are being changed so that the two different strings are first tuned together, and then returned to their original resonating frequencies. If we then apply the adiabatic theorem, we would predict that whatever vibrations are in the strings now are the same as the vibrations in the strings that we started with.

However, Xu’s research group discovered that this is not always the case in a system that has some amount of friction. In rare situations that involve the “exceptional point” in parameter space, the energy can end up transferring from the first string to the second string. Every time the parameters were changed counter-clockwise around the exceptional point, they found drastic changes to the final systems. They found that whenever the parameters created a path that encircled the exceptional point, this change happened, regardless of the actual shape of the path.
Teleporting between different sheets
Exceptional points are fairly difficult to imagine for a good reason: They are the result of two 2D sheets intersecting each other in a 4D space. One way to picture these exceptional points is a fire pole connecting two floors of a fire station. While each floor is distinct, they “meet” at the fire pole. However, oddly, when you walk counter-clockwise around the pole on the first floor, you would find yourself on the second floor, without having climbed the pole at all! The phenomenon here is due to the bizarre spatial geometry, similar to shapes like a Mobius strip or a Klein bottle. The exceptional points are mathematically similar, connecting surfaces that appear to be separated.
The example with the fire station may be hard to visualize, but the actual experiment is even more abstract, as there is no actual movement around anything. Instead, when the parameters of the vibrations travel in this loop, the energy of the system shifts. The experimental group was able to quantitatively measure the energy differences in this single membrane by spying on the vibrations with a low-powered laser even as a high-powered laser changed the parameters. This research, the first of its type, provides solid evidence that the mathematicians were right: Exceptional points exist in parameter space, and physicists can utilize them to control the system.
In the same issue of Nature, a separate group also published on this topic, but the group used a completely different method. While the Yale group was able to dynamically change the vibrations using the laser, a group from the Vienna University of Technology led by Jorg Doppler found similar effects through pre-fabricated waveguides, which are equally impressive in the ability to control waves. Together with the Xu research, these experiments provide the first empirical proof of exceptional points.

Taking control of our world
The most powerful implication of this new research may be in its application for controlling systems. The adiabatic theorem, as well as this extension of the theorem, are particularly robust. They do not seem to care what path you take, as long as you return to the same position. This property is analogous to blindly driving through a dark two-lane icy tunnel, but finding that you always end up on the right side of the road at the end. These robust theorems are extremely helpful for experiments, especially in preventing disruptions to the system. “It’s a new type of control over really pristine systems,” Harris said.
Even the classical adiabatic theorem and its offshoots are being used to predict magnetic effects and provide a deeper understanding for many quantum phenomena. This new extension of the adiabatic theorem will provide insight for physicists as they apply it to other systems, like NMRs and MRIs. In fact, this extended adiabatic theorem, as a fundamental physical theorem, could be more broadly applied to any system — so this research could theoretically be applied to anything that can be modeled as a system. However, this isn’t the end of the line on this research for the Harris lab; they have a paper forthcoming regarding the application of this technique to very different kinds of vibrations.
Our understanding of every branch of science is constantly evolving and changing. Just when we think we understand everything about a field, we realize that particles can interact with themselves, that the fabric of space and time can stretch, and that the universe is expanding. Classical mechanics is no different; the extended adiabatic theorem from this study shows just that. At a certain point, we might as well expect to be surprised. If you find yourself walking around a fire pole on the first floor and ending up on the second, don’t be alarmed. Bizarre Twilight Zone scenarios like that are what can help physicist control, bend, and structure our world — no matter how strange those truths may be.
Further Reading:
Doppler, Jörg et al. “Dynamically Encircling an Exceptional Point for Asymmetric Mode Switching.” Nature 537.7618 (2016): 76–79. Web.
About the Author:
Chunyang Ding is a sophomore Intensive Physics major in Saybrook. He serves as Operations Manager for the Yale Scientific and as Yale’s co-Head Delegate to the Ivy Council, and is always boundlessly curious about our remarkable world.
Acknowledgements:
The author would like to thank Professor Harris for his time and enthusiasm in discussing his research

