Art by Ellie Gabriel.
Every day, hundreds of Yale students take classes in Davies Auditorium and work in the Center for Engineering, Innovation, and Design. Likely only several will know that just a few stories above them—on the 4th floor of Becton Center—reside some of the world’s most powerful quantum computers. These devices are housed in the Yale Quantronics Laboratory—Qulab for short—and are operated by cooling superconducting circuits in microwave cavities down to millikelvin temperatures, at which point their behavior is aptly described by the laws of quantum mechanics.
First proposed in the 1980s by physicist Richard Feynman, using quantum mechanical systems (such as atoms) for computation is not a new concept. Much of the progress in experimentally implementing these devices, however, has come in the last twenty years, with superconducting circuits (behaving as artificial atoms) emerging as a leading platform for quantum information processing. Unfortunately, quantum bits, or qubits, built from these circuits are still highly sensitive to various types of noise from the environment. This has driven widespread effort in the field to build better qubits. Recently, a team of researchers at Qulab—led by principal investigator Michel Devoret and graduate student Clarke Smith—designed a new type of protected superconducting qubit that is robust at the hardware-level against several different noise channels.
Notions of Quantum Computing
Quantum computers are based on a fundamentally different set of rules than so-called classical computers—a broad label characterizing most devices in use today. Classical data are stored in bits, and a single binary digit can take on two logical values: 0 or 1. In practice, this could be realized by the passage of current, and the lack thereof, through a wire, or by the magnetization state of a small region of a hard drive. At the lowest level, under many layers of abstraction, all classical algorithms and operations reduce to manipulating some pattern of bit strings from an input state to an output state. The key takeaway here is that bits take on definite values.
In contrast, quantum computers encode information in the quantum states of a system—for instance, in the states representing the lowest two energy levels of an atom. These two states, which we can abstractly label as |0⟩ and |1⟩, form what is known as qubit subspace, and by sending appropriate pulses of light to the atom, one can perform logical operations on the qubit. The key difference from the classical model, however, is that we can also form admixturesof the two states, called superpositions, of the form ????|0⟩ + ????|1⟩. The outcomes of measuring such superposition states are determined by rules of probability, giving either |0⟩ and |1⟩ with probabilities |????|2 and |????|2 respectively. While this may seem counterintuitive, it turns out that several classes of problems are very well-suited to a quantum computer that does not have definite 0 or 1 bits. Some notable examples include cryptography and prime number factorization, optimization and machine learning, and simulating quantum mechanical systems (such as molecules) for applications in fundamental physics and chemistry. However, the aforementioned sensitivity of quantum information means that quantum computers are also more susceptible to noise and other errors that arise from coupling to the environment. Any spurious interaction can lead to unwanted changes to the desired quantum state, and thus introduces errors into a calculation.
The fragility of quantum information has led to what Michel Devoret describes as a two-pronged effort in the field. “The first approach is to discover a better method for quantum error correction […] while the second [approach] is to design physical qubits with better lifetimes and faster gate operations,” Devoret said. Research into quantum error correction (QEC) involves finding ways to encode a logical bit of quantum information across many physical qubits—the benefit is then that the information becomes more robust to noise, being distributed non-locally across the system. However, these kinds of QEC protocols are often very theoretical in nature, and the authors of the present study chose to focus on the more tractable second approach: engineering qubits to have properties that make them less susceptible to noise.
Building Better Qubits
Ultimately, the researchers would develop a novel type of superconducting qubit better protected against noise, which Devoret and coworkers recently reported. The new design is based on a proposed circuit element that allows only pairs of Cooper-pairs of electrons to tunnel across the circuit. “It is an elaboration on the transmon and fluxonium qubits that we had previously worked on,” noted Devoret.
The idea of building qubits from superconducting circuits was first proposed in 1997; progress in the field followed rapidly. In such quantum electromagnetic circuits, charge carriers are pairs of bound electrons—known as Cooper pairs—which may quantum mechanically tunnel through a junction. The quantum mechanical states of the circuit can be labelled by the number N of Cooper pairs that tunnel. Although these circuits are macroscopic objects—made up of many millions of electrons and atoms—the number of effective degrees of freedom is quite small. This gives superconducting qubits a relatively simple energy spectrum and is why these systems are often referred to as artificial atoms.
The transmon qubit, shown in Fig. 1a, is one such type of superconducting qubit, and it is the qubit of choice for many of the commercial players in the field of quantum information, including IBM, Rigetti, and Google. It consists of a nonlinear inductance—the Josephson junction, marked by a crossed box—in parallel with a capacitor, where the charging energy of the circuit is much smaller than the so-called tunnelling energy. The transmon has a oscillating potential energy U = EJ cos(????), plotted in Fig. 1c, where ???? is the superconducting phase in the circuit, and EJ is the tunneling energy for the Cooper pairs across the junction. “The Josephson junction is very precious [in superconducting quantum computing] because it is the only non-dissipative [lossless] nonlinear element we have,” explained Xu Xiao, one of the researchers on the project. “The cosine potential is therefore the only kind of nonlinearity we usually have access to,” Xiao continued. This nonlinearity—stemming from the cosine potential of the Josephson junction—is necessary to ensure that the (frequency) level-spacing is unequal; this makes it possible to address only the lowest two-levels as a qubit, without exciting the higher energy level states.
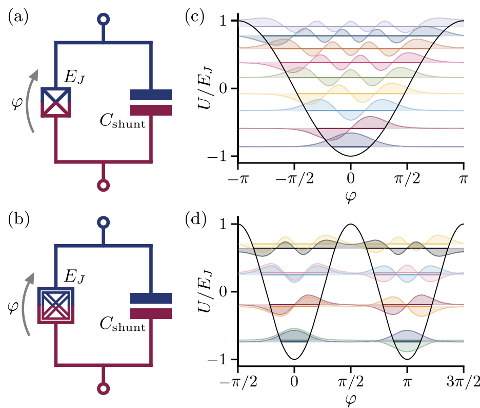
Fig 1: (Reprinted from Ref [1]). (a) Circuit diagrams of (a) the standard transmon, and (b) the novel qubit design based on two-Cooper pair tunneling, where the Josephson junction (crossed box of the transmon) is replaced by a cross-hatched box to denote the new circuit element. The potential energy curves (in black) and corresponding quantized states (in color) are plotted in (c) and (d) for the transmon and new design, respectively.
The proposed “two-Cooper-pair” qubit is shown in Figs. 1b and 1d. Here, the cross-hatched box denotes a novel circuit element which is itself composed of two Josephson junctions in a loop. The current through this loop is controlled by an external magnetic field or flux, which, when tuned carefully, gives rise to an effective potential energy term of the form U = EJ cos(2????), i.e. it now has two energy wells, rather than one. Thus, by connecting several Josephson junctions, it is possible to engineer an effective potential that would not otherwise have been realizable using a single transmon qubit alone.
The “cos(2????)” potential reflects the feature that only pairs of Cooper-pair electrons can tunnel across the circuit element at a time. It follows that the number N of Cooper-pairs that have tunneled must have constant parity (i.e. be even or odd), leading to two different ground states (of equal energy but opposite parity). These degenerateground states—of equal energy—can be used to store quantum information in a way that is resistant towards noise. Like discussed earlier, this system protects its quantum information by distributing it across more than one state. “In experiments, there are various noise channels, which couple to the system via some operator. Because of the special parity of this new potential, transitions via many such noise channels between the logical zero and one states are prohibited,” Xiao said. The researchers at Qulab tested this new design in simulations to show that the characteristic lifetimes of the “two-Cooper-pair” qubit are competitive with other state-of-the-art implementations, at around one millisecond. “This [result] shows how much we can gain […] it seems like if we build more complex circuits, we could go a long way towards building better qubits,” Devoret said.
Outlook and Implications
“I think the field as a whole is realizing how to exploit the specific features of a quantum system to store information,” said Xiao, when reflecting on the significance of their result. “This work is theoretically quite a successful tactic in understanding how we go from a circuit design to a desired Hamiltonian [a mathematical description of a quantum system], and then to understanding why it is robust,” he continued. “Even though this may not be the ultimate qubit used in a generic quantum computer, it still educates us a lot about what types of resources we have.”
Engineering qubits with better coherence properties can be thought of as a passive form of error correction, in contrast to the explicit active quantum error correction protocols described earlier. “Actually, both methods are needed,” Devoret said, referring to two other articles from Qulab to be published soon. These both try to implement an activeQEC, via two other types of qubit: the Kerr-Cat qubit (that encodes information in the phase space of a harmonic oscillator) and the bridge-state qubit. “This research takes place on various fronts; you get here an example of a concerted effort [in our group] to improve quantum information science,” Devoret continued. Indeed, as the field continues to progress, each of these developments will be crucial steps towards ultimately realizing a scalable and fault-tolerant quantum computing architecture—an idea which, unlike in decades prior, now seems within reach.
About the Author: Shoumik Chowdhury is a junior in Saybrook College studying Mathematics and Physics. In addition to writing for YSM, he works on research at the Yale Quantum Institute and Yale Quantronics Lab and is also co-president of the Society of Physics Students at Yale.
Acknowledgements: The author would like to thank Professor Michel Devoret and Xu Xiao for their time and enthusiasm for talking about their research.
Extra Reading
[1] Smith, W.C., Kou, A., Xiao, X. et al. Superconducting circuit protected by two-Cooper-pair tunneling. npj Quantum Information 6, 8 (2020).
[2] Quantum states are — technically — represented mathematically by vectors in an abstract complex vector space known as a Hilbert space; logical qubit operations are then rotations of these vectors. This description naturally leads to many quantum properties such as superposition. For an accessible non-technical introduction to these ideas, see Refs. [3] and [4].
[3] Andy Matuschak and Michael A. Nielsen, “Quantum Computing for the Very Curious”, https://quantum.country/qcvc, San Francisco (2019).
[4] Nielsen, M.A. and Chuang, I., 2002. Quantum computation and quantum information.
[5] Shnirman, A., Schön, G. and Hermon, Z., 1997. Quantum manipulations of small Josephson junctions. Physical Review Letters, 79(12), p.2371.
[6] Devoret, M.H., 1995. Quantum fluctuations in electrical circuits. Les Houches, Session LXIII, 7(8).