While experiencing the pains of waiting for flight transfers or buses that seem to circle around and around, it’s only natural to wish for direct routes. We may not be getting direct routes anytime soon, but researchers in Japan have demonstrated that our traveling woes might be partially solved by looking at slime molds.
A Transportation Conundrum
It’s not that hard to fathom that a network filled with direct routes would be quite expensive to build, but just how expensive or difficult would it be to design a cheap network that still had decent travel times? Imagine a region with eight cities. After conducting initial studies accounting for geography, distance, and many other factors, you find a set of possible roads and their respective relative costs labeled (as shown in Figure 1).
You are in charge of laying down tracks between cities. Your first priority might be to connect all the cities, with the lowest cost. Note that with eight cities, the minimum number of connections required to connect all the cities is seven. To find out how much your rail system costs, just add up all the numbers along the tracks that you decided to lay down. Mathematicians call such a connection a minimum spanning tree (MST).
Though MSTs give you the cheapest rail system, you probably want to consider your customer’s happiness—you can’t give them direct routes but you can certainly try to give them as direct of a route as possible, minimizing their travel times. In the rail system above, there are clearly some paths that take much longer than necessary. Assuming that the costs are roughly proportional to the distance between points, to get from A to B in the above figure, you would have to travel a distance of ~30+35+40 = 105 instead of a direct route distance of 45! One could hardly call this efficient. So the cheapest rail system may not be prudent, and you may consider adding a direct connection between A and B.
One last concern is resistance to failure. As shown in Figure 2, if any of the seven links are cut, at least one city would be left stranded. If we measure “robustness” to considering single failures (as opposed to say, robustness against mass network-wide failure), we say the above network has 0% fault tolerance. Meanwhile, if we add a node between A and B, resulting in eight connections total, only four connections would still cause failure, and the fault tolerance rises to 50%.
Playing around with this network, we see that an optimal solution is highly dependent on the situation and constraints that we would like to consider. Further, the traits that we want in a “good” network necessarily compete with each other. And there would inevitably be more constraints imposed by the realities and politics of everyday life. It would be more correct to say that there is no correct answer.
The Slimy Network Engineer
So how should we go about developing a new transportation system, or any connected network? Researchers led by Toshiyuki Nakagaki, a professor at the Research Institute for Electronic Science in Hokkaido, Japan, suggest that we look to biology for answers. “Biological networks have been honed by many cycles of evolutionary selection pressure,” the researchers argue, and thus “are likely to yield reasonable solutions.” What is their source of inspiration? Slime molds!
Slime molds, such as the Physarum polycephalum that the researchers used, are a good model for transportation networks—their entire body is made of proteoplasmic strands that are made to stream cytoplasm at high speeds. If observed carefully, cytoplasm can reach speeds up to 1.35 mm per second, which is actually among the highest speeds for micro-organisms.
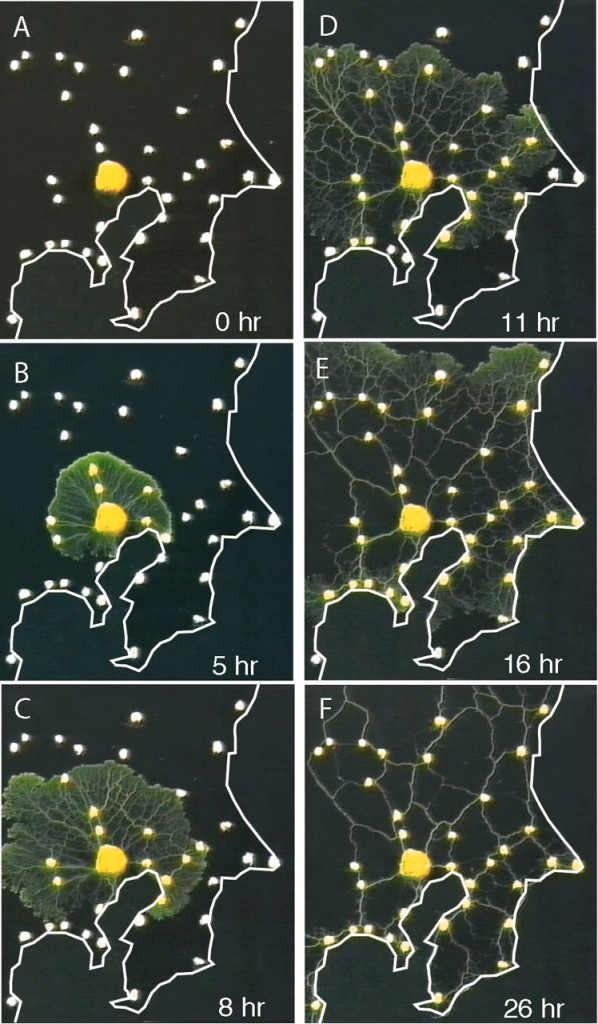
The researchers took advantage of the way slime molds eat. When searching for food, Physarum polycephalum grows a dense network of thin strands over its media. Then, the tubes that carry more nutrients expand while the other tubes contract until they disappear. In this way, the slime mold is able to pare down its tendrils into an efficient network for transporting food.
In particular, the researchers placed oat flakes on agar plates to represent the locations of cities in Japan, with extra oat flakes placed at Tokyo to represent the city’s importance. Using light, which Physarm polycephalum tries to avoid while it grows, the researchers were able to recreate geographical constraints like lakes and mountains. The slime mold was started on Tokyo, then allowed to grow for 26 hours, giving the slime mold enough time to “search out” the plate and pare down its network into several main tubes (see Figure 3).
When compared to the actual rail network surrounding Tokyo, the researchers found that the tubular networks that Physarum created performed remarkably similar to that of the actual rail network (see Figure 4), in terms of cost, efficiency, and fault tolerance. Additionally, when the researchers extrapolated Physarum behavior into a mathematical model, they were able to generate networks that performed marginally better than the actual rail network itself.
“Decentralized” Engineering
The result is even more remarkable in that slime molds, and thus the mathematical model as well, represent a “decentralized” paradigm of engineering, and the researchers commented that decentralized control “may represent a readily scalable solution for growing networks in general.”
Centralized control is typical of how we solve most of our problems. Imagine a giant team-game of tic-tac-toe where you can only see your own box, and you can only talk to the team members immediately to the sides of you. If your team were in charge of laying down Xs in this game, how would your team coordinate with one another? A natural response would be to pass all the information to one person, who is then in charge of collecting all the information and making a decision. Your team would be hard pressed to play the game without someone being able to “see” everything that is going on.
Yet as the slime mold grows, a tendril in say, its left arm has no idea what’s happening in the right arm, nor does the slime mold have a centralized brain that can coordinate all the other arms. Instead, each tendril modifies its own grown according to information it has about its own food transport rate. This is what the researchers mean when they refer to “decentralized control.” It requires significantly less computational power, and in the case of the slime mold, literally lends itself to “growing.”
Looking Towards Applications
Biology is proving to be an appealing and rich source of inspiration for many engineering problems, particularly because over time evolution has developed many cheap, efficient design paradigms that differ greatly from how we have traditionally tackled problems. That said, there is still much to be researched. We are still unsure how exactly Physarum transports or grows, just as we are unsure why the mathematical model the researchers generated should quantitatively look like the Tokyo network.
Is the model flexible enough to create other kinds of networks, with other properties? Previous research has shown that many natural networks, like vascular systems and river networks, may have developed as the result of minimizing energy loss. Could Physarumbe minimizing energy loss of nutrient transport? We still need to understand the exact optimization problems that slime molds can solve, so that we do not blindly apply techniques we learn from slime molds to tackle challenges that they are poorly suited for.
