In 2011, Canadian tech company D-Wave stunned the world by announcing that it would market a functioning quantum computer. Soon, companies ranging from Google to NASA bought versions of the device, and scientists began scrambling to evaluate what potentially was the biggest technological breakthrough of the century. One third-party test, in which the new quantum computer solved a complex math problem 3,600 times faster than a cutting-edge IBM supercomputer, seemed to substantiate D-Wave’s claims of quantum computation. Other tests found no evidence of quantum activity at all.
Quantum computing, an idea which has captivated physicists and computer scientists alike since its conception in the 1980s, has proven difficult to realize in practice. Because quantum computers rely on the uncertainty built into the laws of quantum physics, they are extremely sensitive to their environments. A small imperfection in even a single component of the design can be devastating. One technical challenge is that heat energy can disrupt the fragile quantum states, so quantum technology is usually cooled almost to absolute zero (-273 degrees Celsius). D-Wave’s quantum computer is small enough to hold in the palm of your hand but has to be housed in a 10-foot-tall refrigerator.
Yale researchers, led by Professor of Electrical Engineering and Physics Hong Tang, have developed a new version of a device called a piezo-optomechanical resonator that could allow quantum computers to operate at higher temperatures. The paper, which is co-authored by graduate students Xu Han and Chang-Ling Zou, describes an improved method of connecting information in physical and electrical domains. This advance could be used as the basis for reliable memory storage for quantum computers—an important step towards stronger quantum computing.

From Schrodinger’s cat to national security
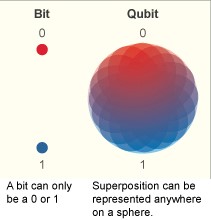
Quantum computing fundamentally differs from classical computing in that it relies on the non-intuitive quantum properties of light and matter. In familiar classical computation, information is stored as bits which can take on the values 0 and 1—they are simple on/off electrical switches, and it is easy to check their positions. The computer then performs tasks using sequences of logical operations on the bits. For example, it might say that if bit A is 0, then bit B should be set to 0, but if bit A is 1, then bit B should be set to 1; or that bit C should be set to 1 only if bits A and B are different.
In quantum computing, by contrast, the situation is not so straightforward. First of all, information is stored in qubits (short for “quantum bits”) which have more than two possible values: 0, 1, and a combination of 0 and 1. These qubits are particles with distinct measurable quantum states corresponding to “0” and “1,” but one of the principles of quantum physics is that sometimes we can predict the result of a measurement only in terms of probabilities. So in quantum mechanics, even though sometimes we might know that we will always measure the particle as “0,” there can also exist a scenario in which there is a 50 percent chance of finding the particle in the “0” state and a 50 percent chance of finding it in the “1” state. The surprising part is that, mathematically speaking, the latter particle is actually in both states equally until we measure it as being in one or the other, and it is meaningful to think of such a qubit as having value ½ representing a “mixed” state even though ½ is not a possible measurement.
Another useful property of quantum mechanics called entanglement links the measurements of different particles. For example, if particles A and B are entangled, then we might know that whenever we measure both particles, we will get one “0” and one “1.” In this case, measuring one qubit immediately determines the value of the other, and it is possible to use this property to “teleport” information!
The unique logical underpinnings of quantum computation allow quantum computer to approach old problems in new ways. Since qubits are more complex than regular bits, quantum algorithms are often more streamlined than their classical counterparts, especially when searching for optimal solutions to problems. For example, if we want to find a car that is hidden behind one door out of a million, a classical computer would have to check the doors one by one, and, in the worst-case scenario, it would have to make a million queries. A quantum computer, by contrast, can use a probabilistic algorithm to find the car in at most only a thousand queries.
Quantum computation has potential applications in many problems that would take classical computers longer than the age of the Earth. In the best-known example of this principle of “quantum speedup,” computer scientists have created a quantum algorithm that can factor large numbers (essentially a needle-in-a-haystack problem like the car example above) exponentially faster than is possible for any classical algorithm. Although this problem may not seem very exciting, it in fact underlies many more complex processes such as cryptography. Similar principles apply to choosing cost-effective combinations of building materials and even to identifying keywords for news articles. Unsurprisingly, quantum computation is often the best way to model complex natural systems.
We have made significant progress over the past few decades towards meeting the challenges of quantum computing. As early as the mid-1990s, we have manipulated qubits and written codes to correct spontaneous errors in quantum computers. In the 2000s, we demonstrated long-distance entanglement. In 2013, Hong Tang and his team contributed to the corpus of knowledge when they determined a method for measuring quantum systems without permanently altering them. Now, in 2016, the Tang Lab at Yale has once again expanded the quantum computing toolbox, this time in the stubbornly challenging field of information storage and transfer.
A new approach to quantum memory
You probably carry around in your pocket a crucial piece of the new Yale device: Smartphones contain the materials that Tang and his team used to bridge the mechanical-electrical gap. Piezoelectrics are materials, usually crystals, that accumulate charge when compressed, twisted or bent. For instance, when a piezoelectric sheet is creased, a net negative charge forms at the fold, and net positive charges form at the ends. Conversely, when an external magnetic field causes charges in a piezoelectric to move, the object responds by changing shape physically. In this way, vibrations in physical objects and electrical fields can easily be connected, or, as physicists say, coupled. Piezoelectrics in smartphones often power tiny speakers— they convert electrical signals into sound waves, which arise from physical pulses.
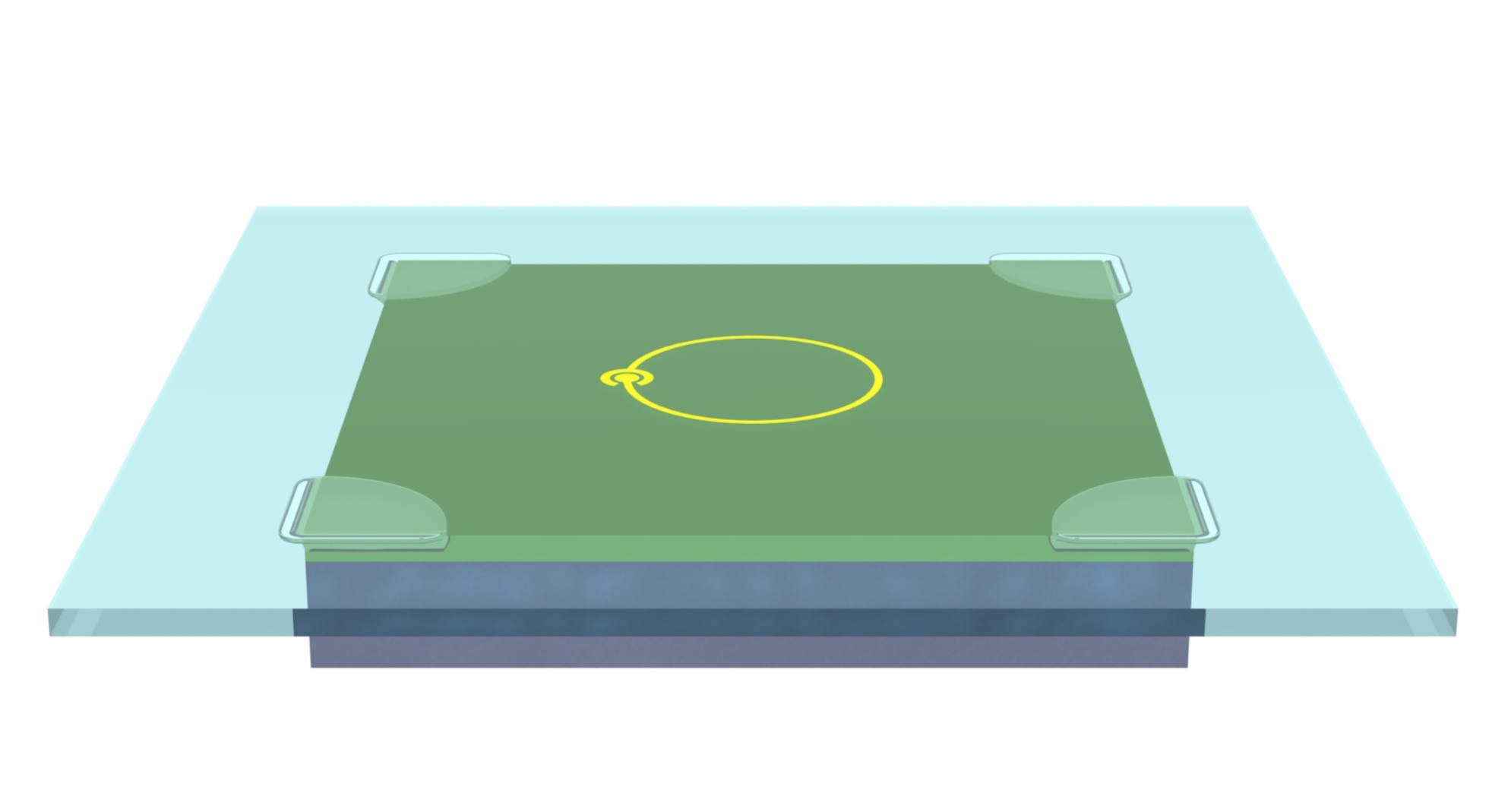
The Yale piezo-optomechanical device consists of a pair of tiny resonators: a silicon wafer and a wire loop situated above it. “It is useful to think of a resonator like a tuning fork because it responds most powerfully to a particular resonant frequency,” said Han, an electrical engineering Ph.D candidate who worked on the project. The two ends of the wire loop do not quite connect, so electrical charges tend to bounce back and forth around the circle, which functions as an electrical resonator in the microwave region of the electromagnetic spectrum. The wafer, which is about as thick as five sheets of paper, functions as an acoustic, or mechanical, resonator. This resonator is coated with a thin layer of aluminum nitride, a piezoelectric material, which facilitates the exchange of oscillations—and energy— between mechanical and electrical components. “If you want to transfer information between two systems, it is necessary to have an efficient coupling mechanism,” Han said.

The idea of coupling between mechanical and microwave electrical domains is not new; the Yale team’s innovation is achieving stronger coupling on a smaller scale. The key is using resonators with a higher frequency: Whereas other designs have used frequencies on the order of a few million oscillations per second, the Yale design runs at ten billion oscillations per second. As a result, the device is solidly in the so-called strong-coupling regime —meaning that the rate of information transfer is greater than the natural energy dissipation rates of the individual systems—and transmitted signals are clearer and longer-lasting. Yet high frequency comes at the cost of increased construction difficulties. “Since the device is small, it is more susceptible to perturbations in the environment,” Tang said. As a result, the design carefully balances considerations of compactness and robustness.
The researchers believe that applications of their breakthrough lie mostly in the far future. “This is fundamental research, so it’s not immediately pertinent to daily life,” Han said. Instead, the piezo-optomechanical resonator’s real value is as a component of more complex systems. Because of the strong coupling achieved, it is well suited for quantum uses where “noise” from ambient heat (analogous to TV static) would otherwise be disruptive. “For high-frequency devices, the temperature requirement is not as low,” Han said. Chang-Ling Zou, a postdoctoral student in Tang’s lab, hopes to develop this strength into a basis for quantum memory storage, which is currently unfeasible at most temperatures. Small vibrating crystals would serve as physical memory, and the resonators would convert between these crystals and the computational part of the computer, which would likely operate in the microwave domain.
The Yale team is also looking to incorporate visible light into their design. “The next step is integrating an optical resonator and using the acoustic resonator as an intermediary between microwave and optics,” Han said. Accomplishing this feat could improve computer signal processing, radio receiving efficiency, and information transmission across long distances via optical fiber cables.
Given its versatility, the piezo-optomechanical resonator may find its way into all kinds of applications. From analyzing the stock market to sending trans-Atlantic messages, you can expect to hear more about this small device in big-time situations.
Further Reading: Ambainis, Andris. “What Can We Do with a Quantum Computer?” Institute for Advanced Study. 2014. Accessed October 27, 2016. https://www.ias.edu/2014/ambainis-quantum-computing.
About the Author: Noah Kravitz is a freshman in Calhoun College. He is interested in studying math, music, physics, and philosophy.
Acknowledgments: The author would like to thank Xu Han, Chang-Ling Zou, and Professor Hong Tang for explaining their research.
Cover image: In this schematic, the thin layer of aluminum nitride allows coupling between the silicon sheet and the wire loop. The lower component of the device could attach to other mechanical components, and the upper part could attach to other microwave components. Image courtesy of Xu Han